【教師注意】數學好玩的趣味情境創設：個體興趣養成的視角

【編者按】無論孔子的“知之者不如好之者，好之者不如樂之者”，還是畢達哥拉斯學派倡導好奇心為根源的“愛智慧”，都指向樂于學習的教育目標。本研究旨在從教師注意視角，通過案例研究，分析如何構建趣味情境，營造興致盎然的輕松數學教育環境，讓孩子在“玩”數學中，將情境興趣轉化成個體興趣。

1. 研究背景

孔子在《論語?雍也》中指出，“知之者不如好之者，好之者不如樂之者”。畢達哥拉斯學派將認識萬物之學定義為“愛智慧”，是激發好奇心，以驚異為根源的精神的生殖力和創造力。但現實中枯燥乏味的數學課堂比比皆是，數學面目可憎，學生興趣索然; 家長輔導孩子數學甚至達到了“劍拔弩張”之情狀。如何營造興致盎然的輕松數學教育環境，似乎成為一個頗具挑戰的社會性話題。

王燦明（2020）研究“李吉林情境教育思想”時指出，對情境教育的不懈探索，讓李吉林越來越重視情感的作用。一開始趣味數學24點100題，她將情感作為情境教學的“動因”，后來又將它看成情境教學的“紐帶”，最后將它視為情境教育理論的“命脈”。因而，以調動學生情緒為中心，激發學生興趣，成為教學情境設置的關鍵，因而趣味情境設置成為本研究中心話題。

2. 理論架構

2.1情境興趣與個體興趣

什么是興趣？赫爾巴特將學習興趣定義為主動性，它與漠不關心相反，是個體在教育中所表現出來的一種欲望沖動。

杜威認為興趣“含有居間的事物的意思 ，即把兩個本來遠離的東西聯結起來的東西”?！芭d趣就是一個人和他的對象融為一體”，興趣是兒童的需要與教學環境的營造。杜威進一步指出，如果我們能夠發現一個兒童的急迫需要和能力，我們又能夠提供一個有材料、有用具、有資料的環境——自然的、社會的和理智的——以指導它們恰當的運作，我們就不需要去考慮興趣。

20世紀90年代初，美國學者海蒂（Hidi，S.）將興趣分為個體興趣（ ）和情境興趣（ ）。個體興趣類似于學生主體因素，一般指個人傾向或偏好，它以人的知識、價值觀及積極感情為基礎，具有相對穩定性和持久性。情境興趣類似于教學環境因素，一般指學生被教學中的某些條件、刺激所吸引，如復雜性、新穎性、不確定性、沖突性等內容，但這種吸引往往不夠穩定或持久。

海蒂認為，從情境興趣到個體興趣，大致要經歷情境興趣的激發、維持、個體興趣的萌芽與成熟四個階段。每一階段各有其獨特的特征、發展趨勢以及促使興趣由低階段向高階段轉化的條件。

2.2 學習興趣與教育相互作用的現象學原理

現象學所研究的既不是單純的主體，也不是單純的客體，而是在主體向客體投射的意向性活動中，主體與客體之間的相互關系以及其所構成的世界。

按照現象學觀點，教育情境是焦點，興趣是邊緣域，兩者之間相互作用過程也可以運用圖1展現出來。

圖1：邊緣域與焦點關系示意圖

從圖1看出，教育影響對個體興趣不能直接產生作用，需要個體能動加工，也就是被認知評價后，才能作用于邊緣域以決定是否形成學習興趣。決定學習興趣的是主體對該教育影響的解讀、評價或歸因。它們之間是情緒建構理論的“激發事件—— 認知評價——情緒結果”關系。海蒂認為，“對事件的認知評價引起并建構了相應的情緒體驗”，而學習中積極的情緒體驗正代表著學習興趣的可能。

3. 案例研究

，Paul（2001）研究顯示，學生學習興趣的養成有賴于激發學生產生“有趣”的體驗，有賴于教育內容對學生來說是重要而有價值的，有賴于教師采取深入淺出或通俗易懂的教學策略，有賴于新舊知識之間的聯系等。本研究從真實教學案例分析出發，探求影響趣味數學情境設置，激發學生個體興趣的可能的教學因素。

標題：從課本到“數學疑云”：柯南再顯身手

懸疑故事引入：（營造情境興趣）

米花町在商店街舉行“首次跑腿”少兒跑腿大賽，參與者們要獨自按照清單上的商品逐一跑腿購買，最快購買完成并返回七點米花公園的小朋友獲勝?！?/p>

柯南和小伙伴組成的少年偵探團作為記錄者參與其中，追隨步美家附近的小宏?？墒窃趨①愡^程中小宏卻被什么人狙擊，離奇失蹤了。（激發好奇心，調動情緒）

柯南他們分頭搜尋商店街終于在一個小路上發現了小宏的身影，正要追上去卻被一輛貨車攔住了去路，只有快速通過四道關卡才能移開貨車追上小宏，他們能否成功幫助小宏脫險呢？

他們需要解決的關卡：

關卡1：找出“漏網之魚”：班上有40個學生，學號分別是1、2、3、…、40。一次數學考試結束后，老師清點試卷時發現竟然只有39張卷子。如果不借助任何工具，僅通過依次查看每張卷子上寫的學號，怎樣才能找出沒交卷的那位同學的學號？

柯南解法：學號和=1+2+3+...+40=820

減去看到的學號

820-學號-...-學號=?

剩下的數就是缺失的那個學號

巧用總和加、減法解決了難題?。ㄈ钟^念激發學生興趣）

關卡2：估算時間：周一早上8:00至9:00之間的某個時刻，爸爸從家出發去上班，此時手表上的時針和分針正好重合。下午2:00至3:00之間的某個時刻，爸爸回到家，此時手表上的時針和分針正好指向完全相反的方向。那么爸爸從出發到回家一共用了多少時間？

（下面的問1、2、3、4、5屬于精巧性提問）

問1：分針走一圈需要60分鐘，時針走一圈需要=720分鐘，能算出分針、時針的速度嗎？

時針速度=360°/720=1/2（度/分）

分針速度=360°/60=6（度/分）

爸爸出發的時刻：上午8:00至9:00之間的某個時刻，時針和分針重合。

問2：從8點開始，需要多少分鐘，分針追上時針？

問3：分針比時針多走幾度？8x30=240度

分針-時針重合所用時間為：240/(6-1/2)=480/11分鐘（除法意義、行程問題意義）

所以爸爸出發時刻是8點480/11分

問4：從2點開始，需要多少分鐘分針追上時針并與時針反向？

問5：分針比時針多走幾度？

2x30+180=240度

分針時針反向狀態所用時間為：240/(6-1/2)=480/11分鐘

所以爸爸回家時刻是14點480/11分

總之，爸爸出發時刻：8點480/11分 爸爸回家時刻：14點480/11分

從出發到回家一共用了：14點480/11分-8點480/11分=6小時（運用真實時鐘圖片，與學生生活場景聯系，建立新舊知識關聯）

關卡3：服藥難題

奶奶每天要同時服用外觀一樣的A、B兩種藥片各一粒。一天，奶奶不小心多倒出了一粒B藥片?，F在她手心上一共有三粒藥片，并且她無法區別哪個是A，哪個是B。請問如何才能嚴格遵循藥方服用藥片趣味數學24點100題，并且不能有任何的浪費？

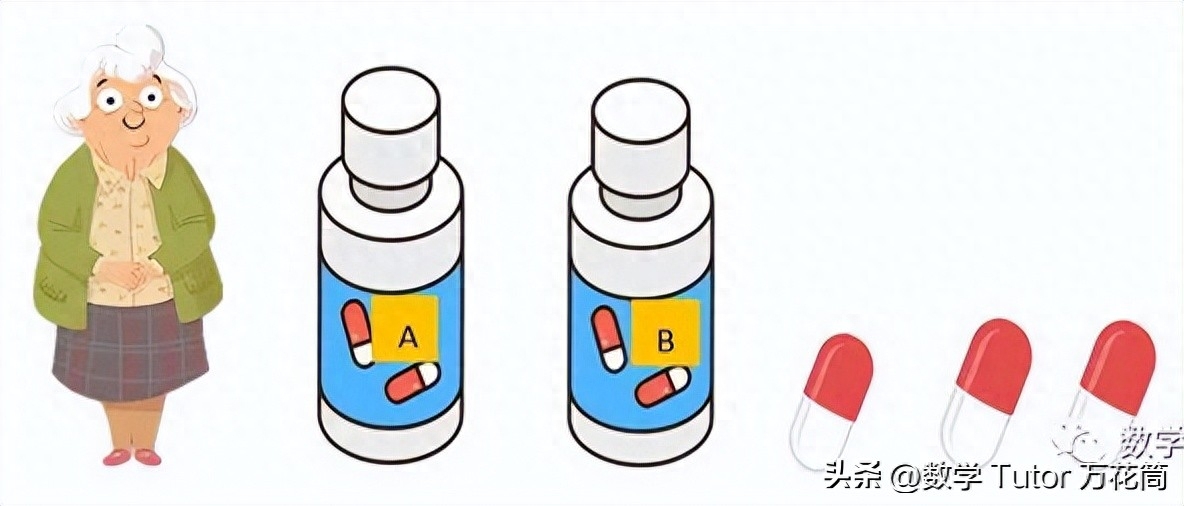
再取出一粒藥片A放在手心

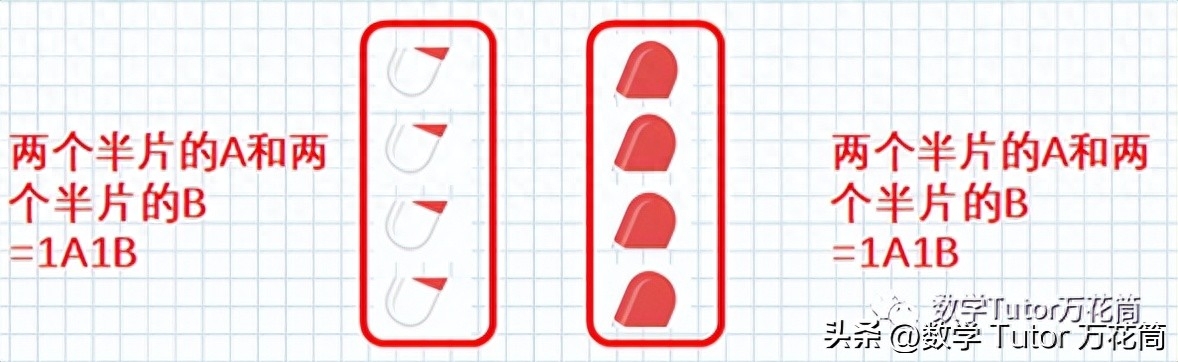
（全局觀念激發興趣，生動圖片展示真實尊老愛幼生活場景，幫助奶奶解決難題，獲得個人成就感體驗）

關卡4：切割游戲

一個長方形蛋糕被切去1個角，還剩幾個角？

討論：

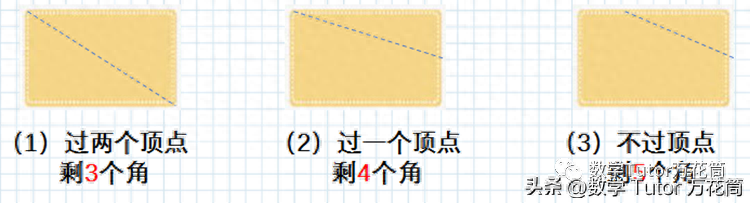
蛋糕角越切越多！（用認知疑惑激發個體興趣萌芽）

故事結尾：柯南成功通過4個關卡，順利幫助小宏脫險啦?。ㄇ昂蠛魬?，維持情境興趣）

4. 教學建議

興趣猶如“一雙看不見的手”，通常居于言說的幕后進行著操作。那么，怎樣的“巧手”才能有利于促進學生的個體興趣的養成呢？

4.1 盡可能建構有豐富個體體驗與評價的教學活動

興趣養成需要經歷情境興趣的激發、維持、個體興趣萌芽、成熟等四個階段。從情境興趣轉化為個體興趣，特別需要個體能動參與。教師應盡可能建構個體參與感、體驗感強的教學活動，扭轉學生對數學枯燥無味的看法，樂于“玩”數學。

4.2 用精巧性提問創設趣味情境

認識到情境興趣與個體興趣的差異趣味數學24點100題，教師注意的關鍵是挖掘學生好奇心，調動學生能動性。平時注重搜集饒有趣味的數學實際問題，并盡可能精巧設計提問，拉近學生生活，啟發思維，從畏懼數學思維的泥潭中走出來，使得“做數學”變得津津有味。

4.3 注重情境與知識的轉化

情境與知識的轉化有利于學生自我評價，是形成個體興趣的關鍵。情境-知識轉化首先以數學概念為基礎，是建立在對概念理解的意義之上。比如本案例研究中關卡2的行程問題、除法的意義。更重要的是體現全局觀價值，站在全局視角看待問題。比如本案例研究中關卡1、3都蘊含全局觀念。不拘泥于細節，從整體出發解決問題，給人豁然開朗感覺的整體觀，讓學生體驗駕馭感、成就感。